私は酒が好きで毎日飲んでいますが、これを心配した妻が次のように言いました。
「来年はせっかくのミレニアムなんだから、あなたのお酒を制限させていただきます。
ある日を解禁デーだとしますね。その前日が解禁デーでなかった場合は翌日も解禁デー、解禁デーだった場合翌日は禁酒デーとします。
また、ある日が禁酒デーだとすると、その前々日が禁酒デーでなかった場合は翌日も禁酒デー、禁酒デーだった場合翌日は解禁デーとします。」
ミレニアムだから何だってんだよ〜!
しかし私はこの妻の言い付けを守ることにしました。
(問題)
西暦 2000 年 1 月 1 日を解禁デーとすると、私は西暦 2000 年に酒を飲むことができる日(解禁デー)は何日あるでしょう?
ただし西暦 2000 年はうるう年です。
西暦 2001 年が楽しみだな〜(爆)
※ 答えが複数ある場合は、小さい順にカンマで区切って答えて下さい。
出題: Hamayan さん
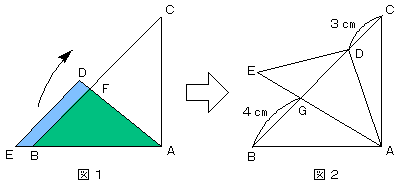
図 1 は大きさの違う 2 つの直角二等辺三角形 ABC、ADE を、点 A および、辺 AB と辺 AE が重なるように置いた図です。ただし、AB = AC、DA = DE で、点 F は辺 BC と辺 AD の交点です。
三角形 ADE を点 A を中心に点 D が辺 BC 上に来るまで時計回りに回転させます。このとき、辺 BC と辺 AE の交点を G とします(図 2)。
BG = 4 cm、DC = 3 cm のとき、図 1 の三角形 ABF と、台形 BFDE の面積比を「三角形 ABF の面積 : 台形 BFDE の面積」の順にできるだけ簡単な整数比で表して下さい。
※ 図は必ずしも正確ではありません。
出題: 長野美光 さん
ここ算数市では、料金体系の違う 2 社のタクシーが競争しています。1 社は算数タクシー(2 km 未満 750 円、以降 500 m 毎に 150 円)、もう 1 社はトライ交通(2 km 未満 700 円、以降 400 m 毎に 100 円、但し毎時 20 km 以下で走行した時は、2 分毎に 100 円を距離料金に加算)です。
さて見栄造さんは今日は給料日だったので、リッチな気分で帰宅にタクシーを使うことにしました。会社の前にたまたまいたのはトライ交通、早速乗り込みました。
しばらくは気持ちよく毎時 60 km で走っていましたが、料金メーターが何回かかわった頃に運悪く渋滞に巻き込まれてしまいました。渋滞の最後尾につけたとき、見栄造さんと同じアパートから自転車(毎時 24 km)で通勤している同僚の走太さんがちょうど真横にいました。
結局丁度 2 km ののろのろ運転(常に毎時 20 km 以下)だった渋滞を抜けた後は家までずっと、すいすいと毎時 60 km で走れました。また、渋滞を抜けてから丁度 10 分後に走太さんの自転車を追い抜きました。
家に着いたので料金メーターを見ると、先月の給料日に乗った算数タクシーの料金とぴったり同じでした。
タクシーは瞬間的な加速減速が出来る、つまり会社の前でドアを閉めた瞬間に毎時 60 km になるし、家の前では毎時 60 km からピタリと止まれるものと仮定して、問題に答えてください。
問題: 走太さんは自転車通勤で、片道何分かかるでしょうか。分未満を切り捨てして整数で答えて下さい。
参考 〜トライ交通に乗ったときの料金の一例〜
5 km の距離を走行し、そのうち 10 分間は毎時 20 km 以下で走行した場合の料金は、1500 + 500 = 2000 円になります。
※ 考えられる数値が 2 つ以上あるときは、その全てを小さい順にカンマで区切って答えて下さい。
例) 10 分 10 秒以上 11 分 30 秒以下、または 20 分以上 20 分 50 秒以下のときは 10,11,20 と解答して下さい。
出題: 中川琢也 さん
平行四辺形 ABCD の内部の点 E を通って辺 AD に平行な直線が辺 AB、辺 CD と交わる点を P、Q、E を通って辺 AB に平行な直線が辺 BC、辺 DA と交わる点を R、S とする。このとき E が △ABD の内部にあれば、
カッコに数字をいれなさい。
出題: 川田智之 さん
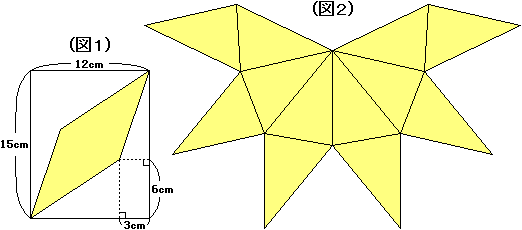
縦 15 cm、横 12 cm の長方形の紙が 6 枚あります。
これら 6 枚の紙から、(図 1)のような平行四辺形を切り取ります。
この 6 つの平行四辺形の紙を(図 2)のように辺どうしでくっつけてみると、合同な 12 個の三角形の面からなる立体の展開図になります。
では、この展開図を組み立ててできる立体の体積は何 cm3 でしょうか。
| (注 1) | 6 つの平行四辺形の貼りつけおよび展開図の組み立ての時ののりしろは考えません。 |
| (注 2) | 図を見れば明らかですが、立体の合同な 12 個の三角形の面の内角はいずれも 90 度より小さいです。 |
| (注 3) | "へこみ" のない立体を考えてください。 |
出題: CRYING DOLPHIN さん
A 君の電卓が、ついにこわれました。テンキーのうち、0 (ゼロ)を除く二つのキーが、別の数字を入力するようになってしまったのです。
この電卓で、
1+2+3+4+5+6+7+8+9
を計算ししたところ、答えは 45
1×2×3×4×5×6×7×8×9
を計算したところ、答えは 725760 になりました。
この電卓で 4321+9876 を計算したときの答えを求めてください。
注: 例えば、1 のキーが 3 を入力し、2・3・4 のキーは正しく入力できるとすると、1+2+3+4 を計算したつもりが 3+2+3+4 を計算するようになります。
出題: ブタゴラス さん
円周上に 14 個の点があります。
2 点を結ぶ線分の交点は、全部でいくつあるでしょうか。
ただし、3 本以上の線分が 1 つの交点を共有することがないものとします。
出題: お金 さん
第 3 回算数トライアスロンが開催されます。
参加者には 1 番から順番にゼッケン番号がつけられています。
参加者の 3 人を選んでそのなかから優勝者がでるという予想をします。そのときどの二人も連続したゼッケン番号でないという条件が、主催者からつけられました。この条件を満たした予想が 156849 通りあることが主催者から発表されました。
ここで問題です。
第 3 回算数トライアスロンの参加者は何人でしょうか。
※ この話はあくまでもフィクションです。念のため。(^^;; (主催者より)
出題: 清川育男 さん
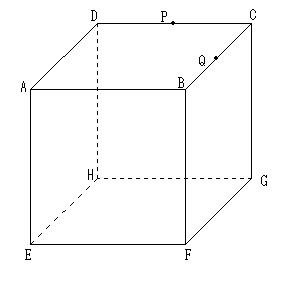
図のような一辺が 3 cm の立方体 ABCD-EFGH があります。
2 点 P、Q はそれぞれ辺 CD、BC の中点です。
3 点 P、Q、H を通る平面で立方体を切断します。
| 【問 1】 | 切断面の面積を求めて下さい。(単位は cm2) |
| 【問 2】 | 切断してできる 2 つの立体のうち、小さい方の立体を考えます。面 PQC 以外のすべての面に接する球の半径を求めてください。(単位は cm) |
※ 設問順にカンマで区切って答えて下さい。
出題: sambaGREEN さん

図のような、9 個の立方体の頂点の位置に固定されたねんど玉があります。このうち 4 個のねんど玉を選び、ひもで結んで四角形を作る場合、
| (1) | 正方形は全部でいくつできますか。 |
| (2) | 何種類の長方形(正方形を除く)ができますか。 |
| (3) | 長方形(正方形を除く)は全部でいくつできますか。 |
※ 設問順にカンマで区切って答えて下さい。
出題: shinei さん
マサルさんとトモエさんが、川の下流 A 地点から上流 B 地点までモーターボートで何往復かする競走をしました。マサルさんが上る速さとトモエさんが下る速さが等しいので、マサルさんの楽勝かと思われましたが、2 台が同時に B 地点を折り返したある瞬間マサルさんのボートがガス欠になり、川の流れに身をまかせるはめになってしまいました。マサルさんは、その後途中でトモエさんに 5 回追い越されながらも、前半のリードがものをいいなんとか同時にゴールイン、めでたく引き分けという結果になったそうです。
さて、この競走で 2 台のボートはそれぞれ水に対してどれだけの距離を走ったのでしょうか。その距離の比を、マサルさんトモエさんの順にもっとも簡単な整数の比で答えてください。
なお、川の流れの速さ、2 台のボートが走る(水に対する)速さは、それぞれ場所や時刻によらず一定とし、また、折り返しのためなどのロスタイムはないものとします。
出題: 中村明海 さん
階段を、1 度に 1 段または 2 段または 3 段ずつ上がる場合を考えます。このとき、階段を 10 段上がる上がり方は何通りありますか。
出題: Shuichi さん
みのるさんの家から駅に向かう途中の陸橋からは、M 遊園地の観覧車がよく見えます。その観覧車にはゴンドラが (A) 台ついていて、一周するのに (B) 分かかります。(ここまで A、B も含めて実話)
(図 1) | (図 2) |
ある日、さきさんがゴンドラに乗ってから、5 台後ろのゴンドラにみのるさんが乗りました(図 1)。その 2 分 10 秒後、さきさんの真下にみのるさんがきました。さらに、その 2 分 30 秒後、みのるさんからさきさんを見ると 15 度上方に見えました(図 2)。
さて、(A)、(B) に当てはまる数はいくつでしょう?
| 注意: | 観覧車の軌道は円で、ゴンドラは円周上の点と考えます。 ゴンドラに乗り込むのは円の真下の一点とします。 |
| ヒント: | M 遊園地に電話すると答えを教えてくれます。(^_^) |
※ (A)、(B) の順にカンマで区切って答えて下さい。
出題: 田村稔 さん
男子校のチャレンジ中学で全校生徒に対してつぎの 2 つのアンケートをおこないました。
集計したところ、1 については 33 人が、2 については 19 人が「いる」と答えました。2 で「いる」と答えたひとのうちチャレンジ中学に通っている弟もいる人は何人いますか。
出題: 中学への算数学コン さん
壁を作ることになり、「うっしー」と「さいころ」はレンガ運びを手伝うことになりました。2 人のレンガ運びの様子は、次のようでありました。
『はじめのうちは、「さいころ」だけが手伝い、ちょうど 30 回分運んだ時「うっしー」も運び始めた。「うっしー」が 4 回運ぶ間に、「さいころ」は 5 回運ぶが、「さいころ」の 3 回分を「うっしー」は 2 回ですます。』
この時、「さいころ」と「うっしー」の運んだ個数が等しくなるのは、「うっしー」が何回運んだ時でしょう?
注: 「うっしー」「さいころ」は人の名前です。(どちらとも実在していますが…。)
出題: うっしー さん
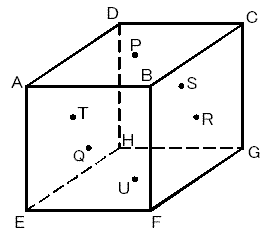
一辺 10 cm の立方体 ABCD-EFGH があり、それぞれの面の中心(対角線の交点)を P、Q、R、S、T、U とします。この立方体の中の 6 つの四角錐、P-EFGH、Q-CDHG、R-AEHD、S-ABFE、T-BCGF、U-ADCB の共通部分(重なる部分)について、次の問いに答えなさい。
| (1) | 共通部分には面がいくつありますか。 |
| (2) | 共通部分の体積は何 cm3 ですか。 |
※ 設問順にカンマで区切って答えて下さい。
出題: ぶぶおパパ さん
4199 (= 13×17×19) 個の箱があります。これらの箱は透明の板で作られていて、中が見えるようになっています。さて、これらの箱の中に一箱に一枚ずつ数字の書いてあるカードを入れていきます。カードに書いてある数字は好き勝手な(正の)整数 (*) です。その後、カードが入った箱を 13×17×19 のブロックに積み上げます。ここで、便宜上、長さ 13、高さ 17の面を正面と呼びます。(もちろん、奥行きが 19 になるわけです。)この時点ではカードの並びはバラバラです。そこで、左下正面から右上奥に向けて中にはいっているカードの数字が大きくなるようにしていこうと思います。つまり、ブロックのどの部分を見ても、左から右に向けて数字が大きくなるように、また、同じように下から上に向けて、手前から奥に向けて数字が大きくなるようにします。但し、次のような手順で箱を並べ換えるものとします:
さて、色々な数字の入れ方や最初の箱の並べ方によって、このような手順で最高何ステップかかることがあるでしょうか?
| 注意 1: | 最高ステップ数のときの数字の入れ方や最初の箱の配置を答える必要はありません。 |
| 注意 2: | このような手順をいくら繰り返しても、望む配置にならないような数字の入れ方、最初の箱の配置がある場合は、答には 0 を入れて下さい。 |
| 注意 3: | 2 回目の第 1 ステップを第 4 ステップ、2 回目の第 2 ステップを第 5 ステップと数えていきます。 |
| (*) | 1 以上の整数をランダムに書いていきます。もちろん、違うカードに同じ数字が書かれることもあるかも知れません。 |
| (**) | 「望みの配置」とは、左下正面から右上奥に向けて数字が大きくなる箱の配置のことです。 |
出題: tomh さん
次の I,K,M からなる表のうち、
| (1) | 「M」の文字はいくつありますか? |
| (2) | 「MIKI」と一直線に読める箇所はいくつありますか? ただし、上下左右と斜めの合計 8 方向のいずれかで読むものとします。 |
( 注意 )
(2) では 1 つの文字を複数で共有することもありえます。
| I | K | I | K | I | K | I | K | I | M | I | K |
| M | I | K | I | I | K | K | K | I | K | I | I |
| I | I | K | M | I | K | I | I | I | K | I | K |
| K | K | K | I | K | I | K | M | K | K | I | I |
| K | I | I | K | I | I | I | I | I | I | K | M |
| I | M | K | I | K | K | K | I | I | K | I | I |
| K | I | I | I | M | I | K | I | K | K | I | K |
| K | K | M | K | K | I | I | K | K | I | I | K |
| I | I | K | K | I | I | K | I | K | I | M | I |
| K | I | I | K | I | M | K | I | I | I | K | K |
| K | I | K | I | K | I | K | I | M | I | K | I |
| I | K | K | I | K | I | M | I | I | K | I | K |
※ 設問順にカンマで区切って答えて下さい。
出題: Miki Sugimoto さん

1 辺の長さが 10 cm の正方形 ABCD があります。
点 M は BC を 2 等分する点です。
点 N は AM を 2 等分する点です。
今、AM と EF が垂直に交わるとき、台形 AEFD の面積を求めなさい。(単位は cm2)
出題: ジンハジメ さん
以下に示す足し算を計算して下さい。

※ 設問順にカンマで区切って答えて下さい。
出題: Nagahiro,Y. さん
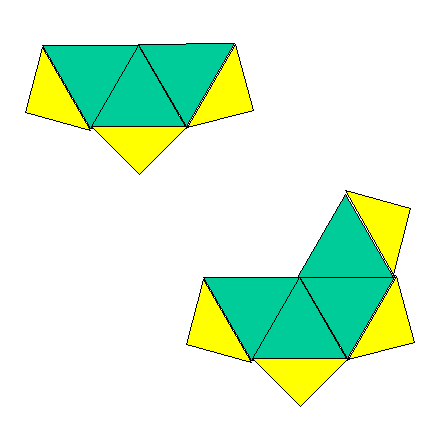
上図は、三つの正三角形と三つの(正三角形の一辺を斜辺とする)直角二等辺三角形であり、下図は、四つの正三角形と四つの(正三角形の一辺を斜辺とする)直角二等辺三角形です。上図と下図の正三角形と直角二等辺三角形は、それぞれ合同です。
図のような折り目で、上図を組み立てたときにできる立体と下図を組み立てたときにできる立体の体積の比は、A : B となります(最も簡単な整数の比であらわしてください)。A、B にあてはまる数を、コロン ( : ) で区切って答えてください(たとえば 1:2 というように)。
出題: せなんな さん
1999 個のボールの中に 1 個だけ他より重いボールが含まれています。天秤ばかりを使って最少 A 回の計量で必ず重いボールを見つけることが出来ます。
また、1217 個のボールの中に 1 個だけ他より重いボールが含まれているときは最少 B 回の計量で必ず見つけることが出来ます。
それでは何個かあるボールの中で 1 個だけ他より重いボールが含まれているとき (A + B) 回の計量でこの重いボールを見つけるにはボールが最多何個のときまでですか?
出題: コスモス さん
算トラ川には橋が架かってませんが、そのかわり何軒かのボート屋があります。ただし、どの店へ行っても「ボートは貸すだけです。元の岸に戻す必要はありませんが、お客さん自身で運転してもらいます。」となってます。
例えば、3 人乗りのボート一艘を 10 人の団体が借りた場合、はじめに 3 人で向こう岸へ渡り、1 人で元の岸に戻り、また 3 人で向こう岸へ渡り、また 1 人で元の岸に戻り‥‥と繰り返し、4 往復半して全員渡りきることになります。この時、片道 2 分掛るボートであれば合計 18 分掛ったことになります。
ある時、A 店と B 店にそれぞれ 80 人の団体が来ました。A 店の 80人は( イ )人乗りを 1 艘、B 店の 80 人は( ロ )人乗りを 1 艘チャーターしました。それぞれどのくらい時間が掛るか聞いてみましたが、A・B どちらの店も「5 人なら 7 分、25 人なら 35 分、50 人なら 77 分掛ります。」という事しか聞けませんでした。
A 店・B 店同時に渡り始め、ともに 2 時間ほど掛りましたが、B 店の方が( ハ )分( ニ )秒速く渡りきりました。5 人、25 人、50 人では A 店も B 店も時間は同じでしたが、80 人では異なったようです。
(イ)、(ロ)、(ハ)、(ニ)に入る数字はそれぞれいくつでしょう?
| ※ | ボートのスピードは、乗ってる人数に関わらず常に一定であるとします。 |
| ※ | 乗り降りに掛る時間は無視します。 |
| ※ | 順にカンマで区切って答えて下さい。 |
出題: シイサン さん
1 から 1999 までの数字を和が 2000 になるように 2 個ずつペアにします。このときできた 999 個のペアについて次の操作を行ないます。
| 1) | ぺアを構成する 2 つの数字をかける。 |
| 2) | かけてできた数字を 12 で割ったとき割り切れるものだけを残す。 |
| 3) | 残ったものについては、さらに 17 で割って割り切れるものだけを残す。 |
★(ここで割り切れるというのは、商が整数になることを指します。)
さて最後に残ったペアは何組あるでしょうか?
出題: TORA さん
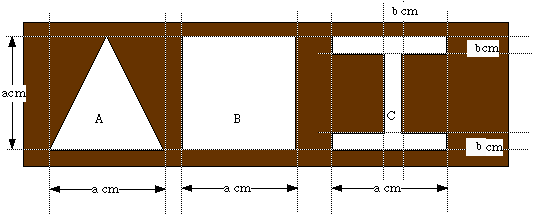
図のような A、B、C という 3 つの穴が開いた板があります。A は底辺が a cm、高さ a cm の二等辺三角形の形をした穴、B は一辺が a cm の正方形の形をした穴、C は幅が b cm の 「エ」 の字の形をした穴で、縦、横ともに a cm で左右対称です。また、a は 50 以下の整数、b も整数です。
横山君はまず、透明で厚さのない板で、この 3 つの穴をすき間なく通り抜けられる体積最大の立体アを作りました。ただし、立体アを穴に通すときは途中で方向を変えずにまっすぐ通すものとします。
次に、この立体アを、底面の角がもっとも少なくなるように地面の上に置き、一番上の面をはがして容器イを作りました。
そして、上から 2 台の水道と合計 30 台のポンプを取り付けて次のような実験をしました。
実験 1: 水道 1 台を使って毎分一定の量の水を入れました。満水の状態からポンプ 5 台で水をくみ出すと空になるまでに 30 分かかり、7 台でくみ出すと空になるまでに 18 分かかりました。
実験 2: 水道 2 台を使って毎分一定の量を入れました。満水の状態から、ある台数のポンプを使って水をくみ出し始め、途中で何度かポンプの台数を変えながら水をくみ出すと、毎分一定の割合で水面が下がりました。
それでは問題です。
(1) 立体アには、面はいくつありますか。
(2) 立体アの体積は何 cm3 でしょうか。
※ 設問順にカンマで区切って答えて下さい。
出題: YokoyaMac さん
かすみさんは正四面体を作ろうと思って紙を用意しました。そこで、できるだけ大きな同じ半径の円を重ならないようにいくつか書きました。1 つの円の中には一辺の長さが半径と同じ正三角形を 6 個作りました。できた正三角形をすべて使って正四面体は 3 個作ることができました。
ここで問題です。書いた円の面積の合計が 615.44 cm2 である時、できた正四面体の体積の合計は何 cm3 ですか。
出題: 算数仙人 さん
+、−、×、÷、および 0 以上の数の書かれたカードがたくさんある。そこから何枚か束にして手元 (A) に置く。
また、これらのカードを積み重ねることができる場所 (B) がある。最初は (B) にはカードは 1 枚も積まれていない。
ここで、次々とカードを手元 (A) の束から引き、次のルールにしたがって操作する。
ここで、手元 (A) のカードを順々に引いて上記操作を行った。引いたカードは順に
11, 12, ÷, 17, 2, 189, 116, 3, +, −, ×, 12 , −, ×, 4, −, ×, −, 8, +, 2660, 2, 30, 12, 25, ×, +, ×, −, ÷, 1999
であった。この結果、(B) に積まれているカードの上から 2 番目の数は一体なんでしょうか。ただし、(B) に積まれているカードが 1 枚である場合には A と、 また積まれているカードがない場合には B と答えなさい。
出題: わかさひ君 さん
ある島は 1607 人の島民から成り立っており、このたび島の代表 者を選ぶことになった。X、Y の 2 名が立候補したが、本人も含めて島民は全員 1 票ずつ投票する権利がある。過半数を確保した者が当選することは普通の選挙と同じだが、この島は地域によって結束が堅いため次のような方法で当選が決まる事になっている。
投票結果は各地域毎に集計され、それぞれの過半数を占めた候補者は、その地域の総意として地域の全票数を一括して自分の票数とする。そして、それらの票数の合計が全島民の過半数を占めると当選する、というものである。(アメリカの大統領選に近いといえる?)
グループは A: 59 人、B: 101 人、C: 205 人、D: 215 人、E: 237 人、F: 291 人、G: 499 人の 7 グループある。例えば A で 30 票、B で 70 票、C で 100 票、D で 120 票、E で 120 票、F で 150 票、G で 240 票取った場合、実際の総得票数は 830 票だが、この島の方式では A、B、D、E、F の総数の和である 903 票を獲得することになるのである。
さて、X 氏は確実に当選するためには最低何票獲得する必要があるか。ただし、棄権票も無効票もないものとする。
出題: ヒデー王子 さん
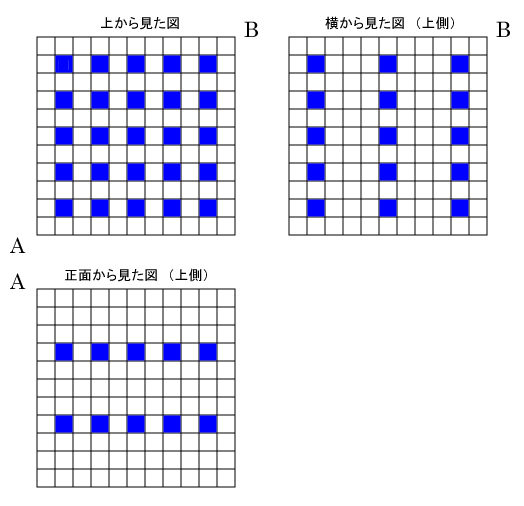
白い立方体と青い立方体を図のように組み立てて、大きな立方体を作りました。この大きな立方体を 4 つの平面で切り取って AB を一辺とする正四面体を作ります。このとき、平面で切り取られた青い立方体 : 平面で切り取られた白い立方体 : 正四面体の中にある完全な青い立方体 の個数の比を求めなさい。ただし、外側から見える青い立方体の位置は向こうの面まで全部青い立方体です。
※ 順にコロンで区切って答えて下さい。
出題: fumio さん

直角二等辺三角形 ABC と直角二等辺三角形 BDE とが、図のように重なっています。辺 AC と辺 BE、辺 DE との交点を、それぞれ点 F、点 G とします。
(1) AB = 30 cm、DE = 20 cm のとき、四角形 FBDG の面積 : 四角形 ABCE の面積 を最も簡単な整数の比で表すと、( ア ) : ( イ )となります。
(2) 三角形 AFE の面積 : 三角形 EGC の面積 を、最も簡単な整数の比で表すと、( ウ ) : ( エ )となります。
( ア )、( イ )、( ウ )、( エ )に入る数は何でしょうか。
※ (ア)、(イ)、(ウ)、(エ)の順にカンマで区切って答えて下さい。
出題: 2人の子供をオンブズマン さん
1 〜 100 までの数を右から小さい順に並べました。
次の操作をほどこします。
| (a) | 並べた列の中から 2 の倍数を取り出し、右から小さい順に並べかえて、もとの列の右端につなぐ。 |
| (b) | 並べかえた列の中の 3 の倍数を取り出し、左から小さい順に並べかえて、もとの列の左端につなぐ。 |
| (c) | 並べかえた列の中の 4 の倍数を取り出し、右から小さい順に並べかえて、もとの列の右端につなぐ。 |
| (d) | 並べかえた列の中の 5 の倍数を取り出し、左から小さい順に並べかえて、もとの列の左端につなぐ。 |
| ‥‥ | |
| (i) | 並べかえた列の中の 10 の倍数を取り出し、右から小さい順に並べかえて、もとの列の右端につなぐ。 |
| (問 1) | この操作をすべて終わったとき、一度も取り出されなかった数字はいくつあるか? |
| (問 2) | この操作をすべて終わったとき、左から数えて 31 番目にある数字はなにか? |
| (問 3) | この操作をすべて終わったとき、ついかして並べかえた列の中の 11 の倍数を取り出し、左から小さい順に並べかえて、もとの列の左端につなぐ。という操作をやったとき「89」は左から数えて、何番目か? |
※ 設問順にカンマで区切って答えて下さい。
出題: KIN さん
マサル王国には代々伝わる秘宝があります。何でも切れる斬鉄剣(第 90 回)や、わずか数個のおもりで 1 g から 40 g まで量れる魔法の天秤(第 71 回)が有名ですが、傾けて使う正六角柱グラス(第 123 回)もその一つです。ところが、トラ帝国が攻めてきて、宝物庫にミサイルが命中してしまいました。
| アキ大臣 | 「王様、大変です。秘宝の六角柱グラスが穴だらけです。」 |
| マサル王 | 「それは困った、春のお水取りの儀式ができないではないか。」 |
| ユー姫 | 「大丈夫です、王様。ほら、穴をふさぐパッチが見つかりました。」 |
| アキ大臣 | 「でかした。でもたった 1 個では.......。どの穴をふさいだらよいものか.....。」 |
(背景はこの程度にしておいて、ここからが問題です。)
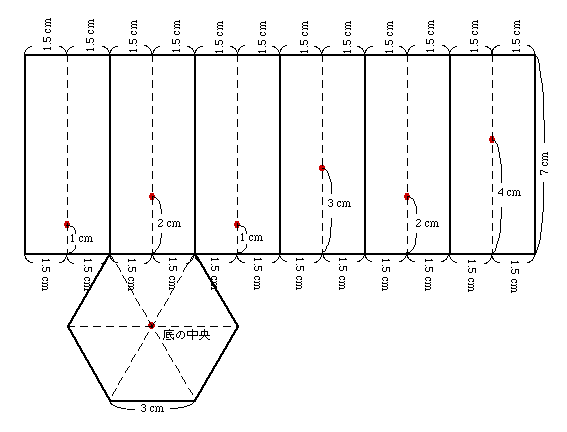
ふたの無い正六角柱型の容器が 2 つあります。2 つの容器は形も大きさも同じで、底辺の正六角形の各辺の長さが 3 cm、容器の高さが 7 cm です。ただし A の容器には、図に示す様に 7 個の小さな穴が空いています(※ 1)。この穴を 1 つだけふさぎ、どこからも水が漏れないように注意して(※ 2)、できるだけ多くの水を入れました。この時、容器を傾けても構いません。
入れた水を、穴の空いていない B の容器に移し替え、B の容器の底が水平になるように置きました。最も深い場合、水の深さは何 cm になるでしょうか。
| ※ 1 | 穴の位置が見やすい様に展開図にしました。正六角柱容器はこれを組み立てた形です。 もちろん 「辺」 の接着部で水が漏れるようなことはありません。 穴を赤丸で表しています。破線は穴の位置を示すためのものです。 穴の大きさや、容器の厚みは無視して下さい。 |
| ※ 2 | 大きさが無視できるほど小さいとは言え、穴が水面下にあると水が漏れてしまいます。 |
出題: ありさのお父さん さん
1999 年も、あと少しで終わろうとしている、12 月 31 日深夜に、A さん・T さん・M さんの 3 人が、賛虎神社の石段下へとやってきました。賛虎神社の拝殿へと続く石段は、長大なことで有名で、昇りきれない人が続出したため、石段と並んで、何処からでも乗り降り自由なエスカレータが設置されています。
石段と、エスカレータの下から上までの段数は、全く同じです。3 人共、歩いて昇る速さは同じで一定です。3 人の歩いて昇る速さと、エスカレータとの速度の比は、12 : 17 です。
さて、3 人は、石段を昇り始めようとしましたが、ここで、お金を持っていないことに気づいたAさんは、近くにある 24 時間営業の ATM でお金をおろして、後から追いかけることになりました。
T さんはエスカレータに乗って歩かず、M さんは石段を歩いて昇り始めました。
1 分 08 秒遅れて、A さんは、エスカレータを歩いて昇り始めました。A さんが昇り始めて 48 秒たった時、M さんに追いつきましたが、その時 T さんは、2 人より 290 段、上にいました。その時点から、A さんと M さんは、エスカレータに乗って歩かず、T さんは、石段を歩いて昇るというように、昇り方を変えました。
やがて、A さんと M さんは、T さんに追いつきました。T さんと M さんが昇り始めてから、A さんが M さんに追いつくまでの時間と、A さんが M さんに追いついてから、A さんと M さんが T さんに追いつくまでの時間は、全く同じでした。
3 人は、ここから一緒にエスカレータを歩いて昇り始めました。3 人一緒に昇り始めて、12 分 24 秒たったとき、人が多くなって、エスカレータが渋滞し歩けなくなったので、3 人は歩かずにエスカレータに乗っていることにしました。
3 人が歩かなくなってから、エスカレータが 2312 段分上昇したところで、2000 年 1 月 1 日 0:00 の時報が鳴り響くと同時に、2000 年問題の影響か、エスカレータが突然動かなくなってしまいました。3 人は、しかたなく、そこからは歩いて昇り、1 日 0 時 12 分 31 秒に、石段の上へと、着きました。
さて、それでは、次の設問にお答え下さい。
| (1) | T さんと M さんが昇り始めてから、石段の上に着くまで、何秒掛かったでしょう? |
| (2) | 賛虎神社の、石段の段数は、何段でしょう? |
| ※ | この問題は、あくまでもフィクションですので、設定等に現実離れしているところがありますが、ご容赦下さい。 |
| ※ | 設問順にカンマで区切って答えて下さい。 |
出題: 溝部光洋 さん
630 を 1 個以上の連続する 0 以上の整数の和で表すとき、何通りの表し方がありますか。例えば、30 を表すと 4 + 5 + 6 + 7 + 8、6 + 7 + 8 + 9、9 + 10 + 11、30 の 4 通りあることになります。
出題: T.Endo さん
次の文で、X に当てはまる数を答えてください。
1 番から N 番まで、それぞれ異なる整数の番号が書かれたカードが、全部で N 枚あるとき、1 枚ずつ取り除いていく手順を次のように決めました。
| (手順 1) | まず、全部のカードを、1 つの円周上に、右回りにだんだん番号が大きくなるように並べます。 |
| (手順 2) | 次に、1 番のカードから、右回りに 1 枚ずつ、続けて 6 枚取り除きます。 |
| (手順 3) | 今取り除いた 6 枚の、次の 1 枚を残して、その次のカードから、1 枚ずつ、続けて 6 枚取り除きます。 |
| (手順 4) | 以下、カードが無くなるまで(手順 3)を繰り返して、次々に 1 枚ずつ取り除いていきます。 |
例えば、N = 53 のとき、取り除かれるカードの番号の順序は、
1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 15, 16, ‥‥, 47, 48, 50, 51, 52, 53, 7, 14, 28, 35, 42, 49, 21
となり、最後に取り除かれるのは 21 番のカードになります。
N = 5764800 のとき、上記の手順で最後に取り除かれるカードは X 番のカードです。
<ヒント>
7×7×7×7×7×7×7×7 = 5764801 です。
出題: サトラ さん
マツダ君の店では、ある日ジュースを仕入れるとき、オレンジとアップルとピーチを同じ数ずつ仕入れました。一本の仕入れ値は、オレンジが 100 円、アップルが 105 円、ピーチが 110 円です。だが、翌日お客がなかなかこないのでマツダ君は次のような計算をしました。
「もし昨日仕入れに使った金額を 3 等分して、3 種類のジュースそれぞれに同額のお金をかけていたら、2 本よけいに仕入れることができたのに‥‥」
では、前日にマツダ君が仕入れたジュースは、全部で何本だったのか。
出題: マツダ さん
お問い合わせは aki(at)angel.ne.jp までどうぞ。