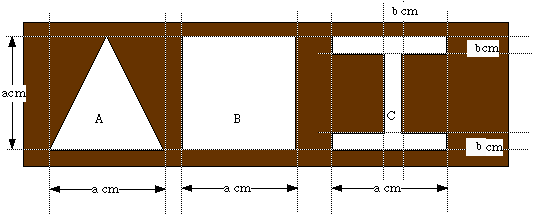
図のような A、B、C という 3 つの穴が開いた板があります。A は底辺が a cm、高さ a cm の二等辺三角形の形をした穴、B は一辺が a cm の正方形の形をした穴、C は幅が b cm の 「エ」 の字の形をした穴で、縦、横ともに a cm で左右対称です。また、a は 50 以下の整数、b も整数です。
横山君はまず、透明で厚さのない板で、この 3 つの穴をすき間なく通り抜けられる体積最大の立体アを作りました。ただし、立体アを穴に通すときは途中で方向を変えずにまっすぐ通すものとします。
次に、この立体アを、底面の角がもっとも少なくなるように地面の上に置き、一番上の面をはがして容器イを作りました。
そして、上から 2 台の水道と合計 30 台のポンプを取り付けて次のような実験をしました。
実験 1: 水道 1 台を使って毎分一定の量の水を入れました。満水の状態からポンプ 5 台で水をくみ出すと空になるまでに 30 分かかり、7 台でくみ出すと空になるまでに 18 分かかりました。
実験 2: 水道 2 台を使って毎分一定の量を入れました。満水の状態から、ある台数のポンプを使って水をくみ出し始め、途中で何度かポンプの台数を変えながら水をくみ出すと、毎分一定の割合で水面が下がりました。
それでは問題です。
(1) 立体アには、面はいくつありますか。
(2) 立体アの体積は何 cm3 でしょうか。
※ 設問順にカンマで区切って答えて下さい。
※ (2)では、考えられるもののうち体積が最大のものを答として下さい。 (12/19付記)
出題: YokoyaMac さん
解答: (1) 11 面 (2) 58000 cm3
解説:
解説図 1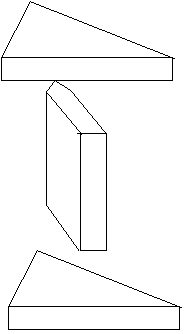 | 解説図 2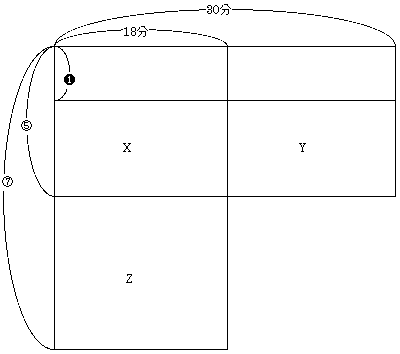 |
(1) 立体Aは解説図1のように、三角柱2つの間に五角柱がはさまったような 形をしている。 適当に面の数を数えると、11面と分かる。 (2) まず、実験1から、解説図2でX+Y=X+Z(ともに、容器の容積を表しますなので)、 水道が毎分出す水の量(白抜きの丸数字1)は、 2台のポンプが毎分くみ出す水の量と等しいことが分かります。 次に、実験2と、aが50以下の整数であること、bも整数であること、 ポンプが合計30台であることから、 aとbの比は5:1, 5:2, 4:1, 3:1のどれかに決まります。 このうち、最もポンプを多く使うのは、 a=50, b=20のときで、立体アの体積は58000cm^3 ちなみに、このとき、ポンプは29台からスタートして途中で適当に 「29 --> 13 --> 29」と変えれば一定の割合で水面が下がります。
お問い合わせは aki(at)angel.ne.jp までどうぞ。